In my last article on option trading I suggested that longer term implied volatility looked rich while short term volatility looked cheap. The strategy that I suggested to extract this value was to buy short-term ATM puts, sell 1 year or greater out of the money puts, and delta hedge the position. I called this getting “Long Gamma and Short Vega”. There were many comments related to simpler strategies on the VIX or via variance swaps for the lucky Europeans who have them to trade, but I maintained that I believe the strategies can be very different because of the flexibility and specificity that options provide.
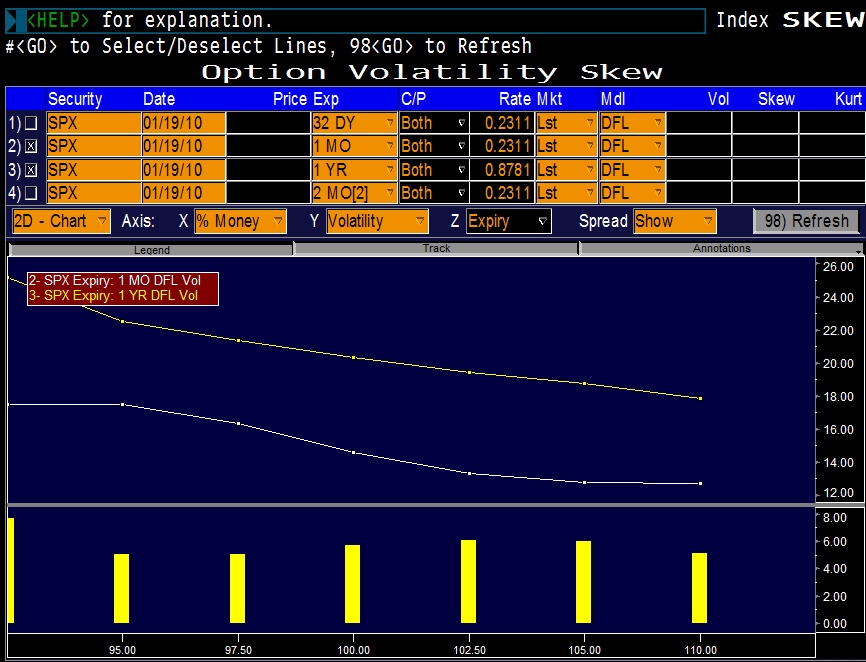
When discussing how to mitigate gamma losses, I used Yahoo as an example, but this time I will explore the S&P 500 because it looks even more ripe for this trade idea. The first thing we need to examine is the option implied volatility skew:
There are two things that you should notice about these curves. The first is that 1 year implied volatility is trading at higher levels than 1 month implied volatility. The second point is that the curves exhibit “reverse skew”, which simply means that the lower strike prices trade at higher implied volatilities than at the higher strike prices. This gives us two takeaways: 1) If we are selling options we would prefer to sell longer dated options (higher implied volatility) 2) when we are buying options we would prefer to buy them at higher strike prices (lower implied volatility).
With these two things in mind comes the strategy that I originally suggested: Long Gamma, Short Vega.
Now that we have the strategy down, let us dissect why it makes sense. From my previous post on mitigating gamma losses, we know that options exhibit large gamma at the money close to expiration. Let us consider a purchased put option on the S&P 500 with a strike price of $1,150:

Gamma spikes dramatically when options are close to expiration and the underlying trades near the strike
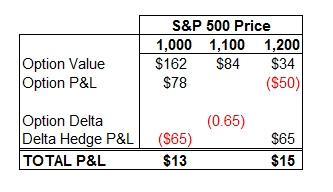
Gamma is what whacks option sellers silly because a written option with a small loss can turn into a very large loss when the option nears expiration and the underlying spikes into the money. In the case of being long gamma, we are happy to see the underlying move rapidly because that means that there is more of a chance that our long option position will end up far in the money. If we are long an option and gamma scalping, we are also happy to see the underlying move quickly because we lock in large gains. This can best be understood with an image:
The important piece to keep in mind when examining the P&L of the delta-hedged position is to remember that you re-balance, or hedge your delta to zero, at discrete points in time. In this example, we assume that you re-hedge when the S&P 500 is at 1,100. The profit of $13 occurs when the S&P 500 falls to 1,000 before you re-balance your hedged position. Likewise, the profit of $15 occurs when the S&P 500 rises to 1,200 before you re-hedge your position. This is just an illustrative example, but it shows that the option gains more when the market falls than the long stock position loses. This happens because the option’s delta gets closer to negative one as the option moves further in the money while your delta hedge position remains constant at 65% of the option notional. In this position, we crave realized volatility for the profitability of the delta-hedged long option strategy.
If we pair a long position in the ATM short-term option, which has a very high gamma, with a short position in an out of the money long-dated option then we still end up with a net positive gamma. This position will only flip-flop to a negative gamma when the market moves towards the out of the money written strike. Therefore, we can scalp gamma in the short-run while having an overall short vega position on longer-dated written option. I will let this idea sink in and leave short vega positions for another time.